-
2579 - 계단 오르기Programming/BackJoon 2023. 3. 16. 13:58728x90
1) 문제 설명
계단을 오르는 데 조건이 있다
계단은 한번에 한 계단 혹은 두 계단씩 오를 수 있다. 한 계단을 밝으면 그 다음 혹은 그 다음 다음 계단을 밟을 수 있다
연속된 세개 계단은 밟을 수 없다
마지막 계단은 반드시 밟아야 한다
2) 문제 이해
조건에 왜 마지막 계단을 밟아야 되는지를 주었는지 모르겠다
일단 dp 문제라고 이해하고, 규칙을 찾아본다
첫번째 계단은
밟거나 밟지 않을 수 있다. (2 계단을 건너뛸 수도 있으므로..)
두번째 계단은
첫번째 계단을 밟고, 또 밟을 수 있다. 그리고 두번째 계단만 밟을 수도 있다.
세번째 계단은
첫번째 계단을 밟고, 2칸을 건너뛴 다음에 세번째를 밟을 수 있고
2번째 계단을 밟고, 3번째 계단을 밟는 경우가 있다.
네번째부터는 점화식을 세울 수 있다
경우 1) 세번째를 밟지않고, 그 이전에는 밟고 자기 자신을 밟을때
경우 2) 세번째, 네번째 계단을 밟고, 3계단 이전 계단을 밟을때
그림으로 표시해보면 더 이해가 쉬운데, 어디를 안밟고 오느냐의 차이이다.

식을 계산해보면 다음과 같다
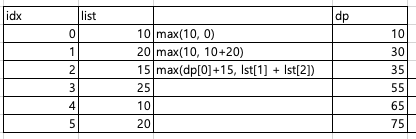
n = int(input()) dp = [0] * n lst = [int(input()) for _ in range(n)] for i in range(n): if i == 0: dp[i] = max(lst[i], 0) elif i == 1: dp[i] = max(lst[1] + lst[0], dp[0]) elif i == 2: dp[i] = max(lst[i] + dp[i-2], lst[2]+lst[1]) else: dp[i] = max(dp[i-2]+lst[i], lst[i]+lst[i-1]+ dp[i-3]) print(dp[-1])'Programming > BackJoon' 카테고리의 다른 글
2225 - 합분해 (0) 2023.03.20 1699 - 제곱수의 합 (0) 2023.03.17 1912 - 연속합 (1) 2023.03.15 1966 - 프린터 큐 (1) 2023.03.15 2156 - 포도주 시식 (0) 2023.03.14